Sundial Park Genk
7. Bifilar sundial
with moondial (R.I.C. Quadrant)
The core of this object is a classical horizontal dial, such as the horizontal dial (nr. 2). The hand-crafted robustness there contrasts nicely to the high-tech sophistication here. The elliptic dial face is generously sized: 100 by 86 cm (39 x 34"). The material and techniques used enabled time lines to be drawn per quarter of an hour. They denote local (solar) time, marked by Roman numerals.
The date is not indicated by the shadow of a fixed point, such as the tip of a pole-style, but by the intersection of the shadows of two separate lines. That is the principle of the bifilar (or cross-wire) sundial. Here, the two lines are the pole-style (the front ridge of the oblique gnomon) and the chain line.
In a horizontal dial with a fixed node (or index) the date line for the equinox is straight, as can be seen in the horizontal dial (nr. 2). Here, the equinox line is slightly curved. The date lines are given per zodiacal month. Next to each date the difference with respect to Greenwich Mean Time is recorded, incorporating the longitude difference (5.5°) as well as the Equation of Time.
Around the pole-style a moon dial has been constructed, so that the time can also be read during nighttime, if the moon is bright enough. The dial face is dated 1998 and depicts the coat of arms of the City of Genk, the geographical coordinates and the motto Aspice, prospice, respice et vale, which means: "Look, look ahead, look back and farewell!"
The sundial has been designed and made by Rafael Soler (Spain).
My comments:
Lack of information
This is quite an odd sundial!
Firstly, nowhere is the information so limited, on the information panel as well as in the brochure. Many strollers coming from the city center will hit upon this dial first. Questions they won't find answered are:
The chain
Then there is the problematic chain. That is the weak spot of this object.
The picture on the top of this page shows the situation on the day of the official opening of the Park, 19 March 2000. The chain does not cross the pole-style at some distance, but touches it: a fixed index.
When we first visited the Sundial Park in July 1998, one month after the official start of the project, there was no chain at all (picture below, left). And the brochure shows it in the the same state. In the picture at the right some benefactor has donated his shoe string - or or was this line added in Photoshop? The picture comes from the Flemish Sundial Society website; no date is stated.
 |
 |
The picture below, also from the Society's site, was made at the start of the project, on 20 June 1988. There the chain clearly passes below the pole-style gnomon, while designer Rafael Soler (left, with book) explains the workings of the moondial to Society President Julien Lyssens.
The documentation at the 1998 start symposium specifies how the chain should be suspended: the bottom point should be 70 mm (almost 3") above the dial face, directly below the tip of the pole-style. In July 2000 we found it in order again, and so it remained on occasional visits since. Perhaps the chain is too easy a target for vandals and therefore no challenge anymore.
The chain line or catenary
The chain line (English: catenary curve) is a most interesting mathematical function. It was discovered in 1691 by Johann Bernoulli, who had been teaching at Groningen University for ten years. The catenary results when a frictionless chain with infinitely small links is suspended from two points. The equation is:
y = y0 + a/2 (ex/a + e-x/a)
The suspension points are here 348 mm apart and 244 mm above the dial face, from which the parameters can be calculated:
y0 = -37.67 mm and a = 107.67 mm.
An important property of the chain line is that the force exerted by its own weight is directed longitudinally at all points, as no transverse forces can remain. This property also holds when the chain line is inverted (and the chain frozen stiff, of course). As such it is used in architecture, for making elegant, strong and thin arches. The arches of Gothic cathedrals were already a practical approximation of this principle, developed by trial and error. A beautiful example of its full potential is the Gateway Arch in St. Louis (USA).
The bifilar principle
The bifilar sundial was invented by the German mathematician Hugo Michnik in 1922. The original design has two horizontal wires above the horizontal dial face. Hence the name; filum is Latin for wire. The upper wire runs north-south and the other east-west. The time is read at the intersection of the two shadow lines.
A special property emerges when the ratio of the heights of the two wires is equal to the sine of the latitude. In that case the pattern of hour lines is homogeneous: the hour lines are spaced at 15°. This is a favorable property: easy to construct, and necessary if one would like to make the sundial adjustable for latitude, summertime and the equation of time.
The above picture shows an example in the Belgian Sundial Village of Rupelmonde, designed by Patric Oyen (Belgium). Oyen's small shadow plane dial can be found at the same crossroads.
Other interesting properties can arise when one of the wires is curved. Designs have been developed with parallel hour lines and/or parallel date lines. An example of the latter, a polar bifilar dial, can be found in Appingedam (Netherlands). A different lay-out of the same principle can be found in Rupelmonde, again constructed by Patric Oyen.
In the bifilar dial in Genk, one wire is the pole-style (as is the case in the above examples), while the other is the catenary. Contrary to the above examples, however, this does not result in any special or interesting hour or date line pattern. The date line pattern is just a trifle different from the traditional horizontal dial, such as nr. 2. For instance, the line for the equinox is not straight, but slightly curved. Not an interesting variation, in my opinion!
The moon dial
The moon dial looks a bit complicated, but reading it is not so difficult. That is, if there is sufficient moonlight available...
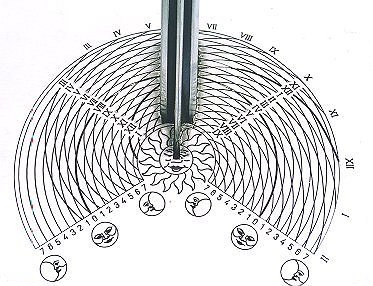
No polished dial faces!
Shadows do hardly show up on highly reflecting, polished metal dial faces (picture below, left). This well-known fact is nevertheless frequently ignored. Is the aesthetic attractivity of such a finish too strong a lure? With a horizontal dial, one may have the opportunity to observe the reflection of the gnomon itself (right). A vertical dial may not allow such acrobatics.
 |
 |
Rafael Soler, sundial designer
Rafael Soler designed many highly creative and exciting sundials. A famous one is the bifilar dial in the Olympic Village in Barcelona (picture). One 'wire' runs horizontal in the meridian plane; the other is a parabola in the east-west plane. Many of Soler's dials can be found on the island of Mallorca; see the webpage of Juan Serra Busquets (in Spanish).