Piet Hein

The Soma cube

The Danish physicist, puzzle inventor and writer Piet Hein (1905-1996) is - among (many) other things - the inventor of the 'Soma cube', which consists of 3x3x3 unit cubes, divided into 7 pieces.

There are 240 essentially different ways to reassemble the cube. Some people have difficulty finding even one solution...
And of course one can try to assemble the 7 pieces into other shapes. Over 2000 have been listed; if you like it, have fun! See the links below.

Some nice sites on the Soma cube:

• The animated solution here is from Jürgen Köller.
  He has them for dozens of games!
• The world's leading sites of Thorleif Bundgård (also on super-ellipse and super-egg) and his companion Courtney McFarren
• Christian Eggermont shows over 50 figures that can be made using the 7 pieces

Martin Gardner's column in Scientific American of September 1958 contributed strongly to the success of the Soma cube. Reprinted in his compilation More Mathematical Puzzles and Diversions, ch. 6. My edition is from Pelican, 1961.

Super-ellipse and super-egg

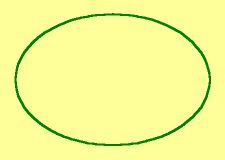
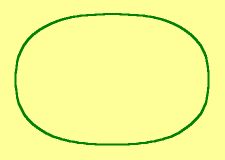
Piet Hein also promoted the 'super-ellipse', a curve that is somewhere in between an ellipse and a rectangle:

Normal ellipse	Super-ellipse

This shape has for instance been used in a traffic circle in Stockholm. It seems to be easier to 'round' such a circle.

When a super-ellipse is rotated around its major axis, a 'super-egg' is formed. A real Columbus' egg, as it can be balanced on one end!

The ellipse and the super-ellipse are special cases of the Lamé curves, named after the French mathematician Gabriel Lamé (1795-1870), who described them in 1818. Hein thus did not 'invent' the super-ellipse, as many seem to believe; he just advocated its usefulness in architecture, the design of furniture and household goods, etc.

The general mathematical form of the Lamé curves is:

    |x/a|ⁿ + |y/b|ⁿ = 1

in which the vertical bars mean that the absolute value is taken. An ellipse results for n=2 (or a circle if a=b). Hein took n=2.5 for his super-ellipse. Other values, like n=2.2 or n=3, also yield pretty curves. I saw some websites stating that Hein used n=3 (for instance Bundgård, mentioned above). I guess that's a mistake.

It is very informative to play around with n yourself. The website of the University of St. Andrews (Scotland) allows you to do so. Great fun!

Martin Gardner's column in Scientific American of September 1965 about super-ellipse and super-egg also is a classic. Reprinted in his compilation Mathematical Carnival, ch. 18. My copy is from Pelican, 1978.

Piet Hein is also the inventor of the helical dial. It can be found in the gardens of Egeskov Castle in Denmark.