Sundials
The equation of time
The equation of time is the difference between the apparent and the mean solar time. The difference has two causes:
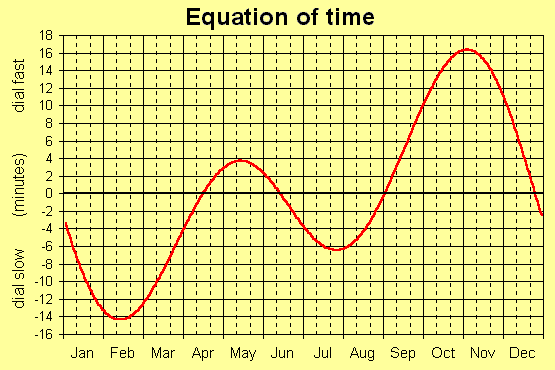
The two effects concur around the winter solstice (December 21). In early November, the sun is over 15 minutes ahead of mean solar time, whereas in mid February it is almost 15 minutes behind. Between the end of November and the end of January, the sun 'loses' about a half minute per day.
This explains why the latest sunrise (on the Northern hemisphere) does not occur on December 21, but a couple of days later; in the Netherlands on December 30. Likewise, the earliest sunset occurs earlier; on December 13 in my country. The difference in both cases is 2 - 3 minutes.
It also explains why the increase in day length in January occurs mainly in the evening. In the Netherlands, the sun sets already half an hour later in mid January than on December 21, but rises only a few minutes earlier.
The equation of time for a given date can be read from the graph below. In case you prefer a table, it's also here. Finally, a formula is given that yields an approximate value.
The values may differ a bit from year to year, up to half a minute, depending on the position in the leap-year cycle. In addition, there is a slow change of the equation of time over the years, due to the precession of the earth.
The problem with corrections like these is always the sign: do you add the correction to one value to obtain the other, or the other way round? The Hubble space telescope provides a notorious example. I stick to the present definition:
+ = the sun(dial) is fast, - = the sun(dial) is slow,
in other words:
mean solar time = apparent solar time (sundial time) - equation of time
Hence, if the equation of time is positive, subtract it from the sundial time to obtain mean time.
If the equation of time is negative, add it to the sundial time to get mean time.
An elegant solution for the sign problem can be obtained for places that are more than 4 degrees away from the standard-time meridian. By adding the correction for longitude to the equation of time, the total correction doesn't change sign anymore.

|
|
Equation of time (in minutes) +: dial fast, subtract table value from sundial reading -: dial slow, add table value to sundial reading |
|||
| Month | 1st | 11th | 21st |
| January | -3.5 | -8.0 | -11.5 |
| February | -13.5 | -14.5 | -13.5 |
| March | -12.5 | -10.0 | -7.0 |
| April | -4.0 | -1.0 | +1.5 |
| May | +3.0 | +3.5 | +3.5 |
| June/td> | +2.0 | +0.5 | -2.0 |
| July | -4.0 | -5.5 | -6.0 |
| August | -6.5 | -5.0 | -3.0 |
| September | 0.0 | +3.5 | +7.0 |
| October | +10.5 | +13.0 | +15.5 |
| November | +16.5 | +16.0 | +14.0 |
| December | +11.0 | +7.0 | +2.0 |
Formula
For on-line calculations, the equation of time E can be approximated by two sine waves, with periods of one year and a half year, resp. The results are accurate to within half a minute.
Assign a number D to the day (January 1 gets D=1, etc, up to D=365 for December 31). The equation of time E is approximately:
E = A1 sin{2 pi (D-F1)/365} + A2 sin{4 pi (D-F2)/365}
The argument of the sine function is expressed in radians.
The constants have the following values:
| period (year) | amplitude (min) | phase (day) | ||
| 1 | A1 | -7.36 | F1 | 4.21 |
| 0.5 | A2 | -9.92 | F2 | -9.90 |
This approximation has been obtained using the data from Savoie (without February 29 and after correction of printing errors).