Analemmatic dials
This page discusses the following subjects:

The principle of the analemmatic dial
We'll start by considering an equatorial dial of the armillary type, such as Genk-1. Choose a certain time, for instance 11 o'clock (local time). At 11 o'clock on different days the shadow of the pole-style always hits the 11 o'clock mark on the hour ring. Which point of the pole-style causes this shadow?
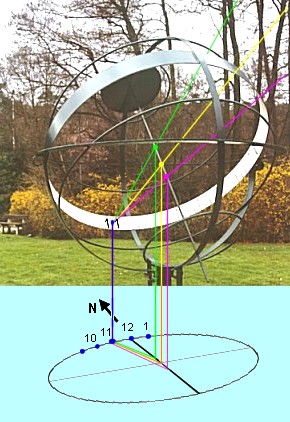 We can find out by drawing a ray of sunlight 'through' the pole-style to the 11 o'clock mark. On the summer solstice (June 21) the sun is high in the sky, and it is the green ray that causes the shadow. On the equinox (March 21 or September 23) the sun is lower and gives the yellow ray. (The hour ring in the picture is closed, so that the front part would block the sun. Just imagine the front is open.) On the winter solstice (December 21) the sun is low and it is the purple ray that causes the shadow on the hour mark.
We can find out by drawing a ray of sunlight 'through' the pole-style to the 11 o'clock mark. On the summer solstice (June 21) the sun is high in the sky, and it is the green ray that causes the shadow. On the equinox (March 21 or September 23) the sun is lower and gives the yellow ray. (The hour ring in the picture is closed, so that the front part would block the sun. Just imagine the front is open.) On the winter solstice (December 21) the sun is low and it is the purple ray that causes the shadow on the hour mark.
In this way a date scale could be constructed along the pole-style, which would run from the green dot (June 21) to the purple dot (December 21) and back again to June 21.
Now project the hour ring vertically onto the ground. The projection is an ellipse, with the major axis running east-west and the minor axis running north-south. The projections of the hour marks are on the ellipse; some are indicated by blue dots. The point for local noon is at the north side, on the minor axis.
Also project the date scale that we constructed along the pole-style, vertically on the ground. And imagine that the vertical green, yellow and purple lines are real rods. On June 21 the shadow of the vertical green rod will just hit the 11 o'clock mark on the ellipse. Likewise, on March 21 and September 23 the 11 o'clock mark will be hit by the shadow of the yellow vertical rod, and on December 21 by the shadow of the purple rod.
Now for the final step: replace the row of vertical rods by a single, movable rod, yourself for instance. When you set yourself at 11 o'clock on the correct point of the date scale, your shadow will hit the 11 o'clock mark on the ellipse.
This figure makes also clear that the hour marks may be extended vertically, as the gnomon is also vertical. That has been done, for instance, at Genk-6. For the same reason the date line may be elevated, so as to elongate your shadow. An example can be found in Leoben.

The shape at different latitudes
It follows from the principle of the analemmatic dial explained above that the shape of the dial depends on latitude. On the equator the ellipse is compressed into an east-west line, with a long north-south date line. Moving to the poles, the date line shrinks and the minor axis of the ellipse increases. On the tropics the two are equal. On the poles, the ellipse would be grown into a circle and the date line shrunk into a point: the equatorial dial is back.
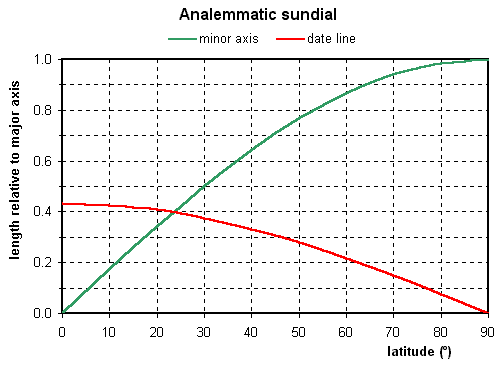
The graph above depicts the length of the minor axis (green) and the date line (red), relative to the major axis, as a function of latitude. The examples below show how the shape comes out at various latitudes. They are constructed for the Northern hemisphere. Local noon is at the top. The 'functional' hour points are filled with red, the others with blue. The date line is divided into the zodiacal months for clarity. The diamond-shaped points are the foci of the ellipse.
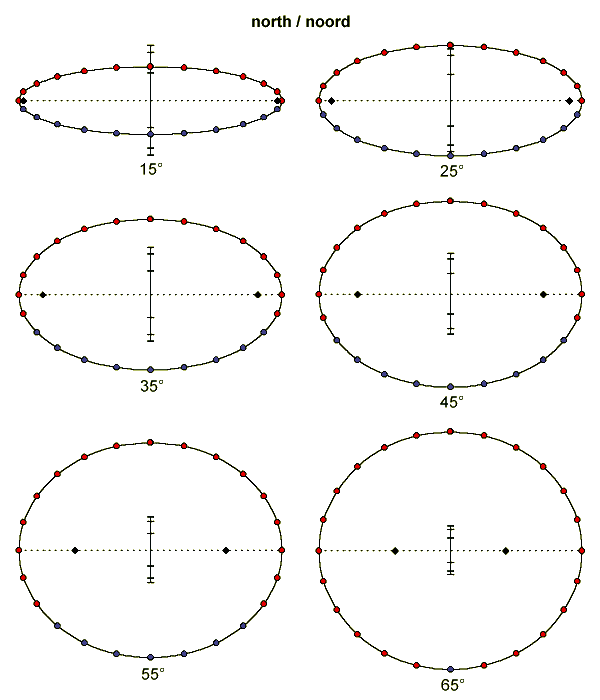
Below 30° your shadow may be quite small. In addition, in summer you have to stand almost on the ellipse. This makes reading the dial very inaccurate. Above 60° the date line is so short that you hardly need a movable gnomon. Hence, the analemmatic dial is most attractive between, say, 35° and 55°. The ca. 50 specimens at this site are all located between 30° and 54°, with the exception of the one in Torreón (ca. 25°).

The human scale
In this section, we consider a human gnomon for the analemmatic dial. How far does his/her shadow reach, extended if necessary by pressing the hands together above the head? How does that turn out at different dates and times and different latitudes?
One may consider the top of the head (or the finger tips) as the index of a nodal dial. During the day, its shadow follows the path usually found in a horizontal nodal dial (see for instance Genk-2). Such a path is usually called a 'date line'. As this phrase means something different in analemmatic dials, let's call it a 'date arc'...
At different dates, the human gnomon stands at different points on the date line, which causes the date arcs to be shifted with respect to each other. How much they shift depends on the length of the date line, which in turn is determined by the size of the dial and by the latitude. We'll have to do some calculations to see how this works out in practice. A spreadsheet program can easily do that.
Let us assume that the gnomon height (top of head or finger tips) is 2 meter (6½ ft). I will compare two values for the major axis, 6 and 10 meter (20 and 33 ft). I chose three latitudes in the most attractive range (see above): 35°, 45° and 55°, and calculated the date arcs per zodiacal month (30° steps along the ecliptic). This is how it looks:
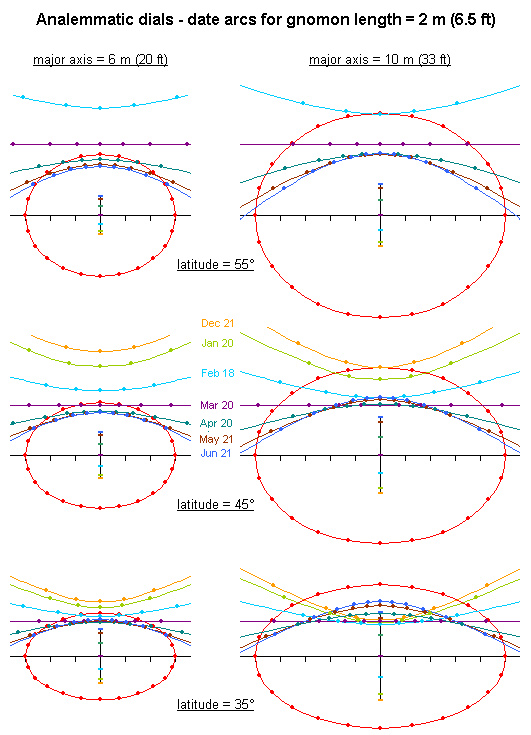
Note that the shadow does not even reach the small ellipse during most of the day in summer. It does not even get halfway in the large ellipse. Of course it's no problem to extend the shadow line, but not too far. The accuracy would decrease, and one would have difficulties reading the hour marks. It would be interesting to investigate how much extension is being tolerated in practice...
In winter the shadow mostly reaches beyond the edge of the ellipse. Then it may be a disadvantage that the shadow is too wide for accurate reading.
Note also that the pattern of date arcs may show interesting variations. In many cases the date arches intersect, so that the shadow has to be extended most on other dates than June 21.
In conclusion, 6 meter (20 ft) is a suitable size, keeping in mind that an analemmatic dial is mostly visited in summer. When the dial is especially intended for use by kids, the size should be reduced accordingly.

No analemma around the date line!
One needs to know the value for the equation of time (EoT) when converting the local time shown by a dial to civil time. Sometimes it is provided as a table or a graph. In an analemmatic dial, it is tempting to take care of the correction by standing aside of the date line when the sun is fast or slow.
This may be the idea behind the analemma that is found around the date line in a quarter of the dials at this site. However, the correction may be right around noon, but then it will be incorrect at other times. The deviations introduced in this way may well exceed the corrections aimed at.
 One should therefore always stand on the date line and not on the analemma, even if that is locally suggested by signs or folders. One may use the analemma to estimate the correction for a given date by measuring the distance to the date line off the noon mark along the ellipse. That is to say, if the designer used that scale, which for instance does not seem to be the case in Brou.
One should therefore always stand on the date line and not on the analemma, even if that is locally suggested by signs or folders. One may use the analemma to estimate the correction for a given date by measuring the distance to the date line off the noon mark along the ellipse. That is to say, if the designer used that scale, which for instance does not seem to be the case in Brou.
The origin of this popular misconception may be the Brou dial, in which the analemma has been added during the 1902 restoration. That was accomplished by the contractor, a sundial amateur. Mayall & Mayall, the authoritative US sundial book, mentioned the alleged function of the analemma without comment (p. 223 in the 2000 edition), including a picture. That may be the reason why this disease is particularly widespread in North America and Australia.
Two exceptions should be mentioned:
The analemma around the date line of Marinus Hagen's dial was provided with a minute scale perpendicular to the date line, from which the correction could be read. In this case the date line doubled as the X-axis for an EoT graph.
The other exception is the dial in Longwood Gardens. The ellipse is split in two halves at the local noon point. Each half has its own figure-8 curve. These do not have the usual analemma shape, but were especially calculated to enable reading of standard time, with an error of one or two minutes.
In general, the analemmatic dial is a typical summer attraction. On the Northern hemisphere, the equation of time is 6 minutes at the most in summer. Hence, in this part of the world the analemmas are completely redundant anyway!

Variations in design
The design of the analemmatic dial can be varied in many ways. Some aspects also refer to other dial types, others only apply to this special type. This is going to be quite a list, then.
Hour points
- local time (noon point on the minor axis)
standard time
daylight saving time (Peize, Lattrop, Hélécine)
standard time including EoT correction (Longwood)
astronomical or Julian time (Besançon)
- subdividions per half-hour (Ootmarsum, Vienne, Avignon) or quarter (Brou, Besançon)
- Arabic or Roman numbers
- only the 'functional' points
all 24 hour points, numbered (Brou, Dijon, Besançon, Gray)
all 24 hour points, only functional points numbered (Murcia)
- times of earliest sunrise and latest sunset (Slijk-Ewijk)
- applied to vertical elements (Genk-6, Hélécine, Mount Annan, Wellington)
- raised, to be used as seat (Kalamazoo)
Date line
Gnomon
Dial face
Other aspects

Circumference of an ellipse
When one is going to construct an analemmatic dial, one has to know how many bricks, tiles etc. to order. So one needs to know the area and the circumference of the elliptic dial face.
For the area of an ellipse there is a simple equation:
A = pi . a . b ,
in which a and b are the semi-major and semi-minor axis, resp. This is a natural generalization of the equation for the area of a circle:
A = pi . r . r ,
in which r is the radius of the circle.
The circumference is quite another story. For the circle it simply is:
C = 2 . pi . r ,
but for the ellipse there is no simple equation. If one tries to derive it, one gets stuck with an unsolvable integral. In fact, the elliptic integrals constitute an important chapter of calculus. Which is not of much help in the building materials store...
Of course, the circumference can be approximated by numerical methods. The graph below presents the circumference as a function of the minor/major axis ratio and is expressed relative to the circumference of the circumscribed circle (radius a).
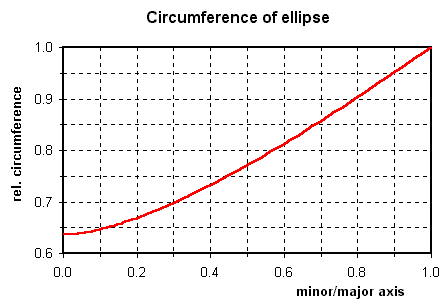
A close approximation (within 0.5%) is obtained by the equation:
C = pi [ 3(a+b) - V{(a+3b).(3a+b)} ] ,
originating from the Indian mathematician Ramanujan (1914). (V denotes the square root.)
Read a moving biographical sketch of this genius.

Websites on analemmatic dials
A number of sites address the analemmatic dial:
Chris Budd & Chris Sangwin, Analemmatic sundials: how to build one and why they work. An extensive, evocative story, in the on-line mathematics journal Plus, June 2000.
John Hoy, Make an analemmatic garden sundial. Simple, easy-to-follow tutorial.
Frederick W. Sawyer, Of analemmas, mean time, and the analemmatic sundial. The story about the sundial in Longwood Gardens, with lots of background info.
Needham Science Center Schoolyard Sundial. The design for your schoolyard dial, for just a couple of $.
Modern Sunclocks (Douglas Hunt), your own analemmatic dial on order! See the specimen in Lafayette (Louisiana, USA).
 We can find out by drawing a ray of sunlight 'through' the pole-style to the 11 o'clock mark. On the summer solstice (June 21) the sun is high in the sky, and it is the green ray that causes the shadow. On the equinox (March 21 or September 23) the sun is lower and gives the yellow ray. (The hour ring in the picture is closed, so that the front part would block the sun. Just imagine the front is open.) On the winter solstice (December 21) the sun is low and it is the purple ray that causes the shadow on the hour mark.
We can find out by drawing a ray of sunlight 'through' the pole-style to the 11 o'clock mark. On the summer solstice (June 21) the sun is high in the sky, and it is the green ray that causes the shadow. On the equinox (March 21 or September 23) the sun is lower and gives the yellow ray. (The hour ring in the picture is closed, so that the front part would block the sun. Just imagine the front is open.) On the winter solstice (December 21) the sun is low and it is the purple ray that causes the shadow on the hour mark.


 One should therefore always stand on the date line and not on the analemma, even if that is locally suggested by signs or folders. One may use the analemma to estimate the correction for a given date by measuring the distance to the date line off the noon mark along the ellipse. That is to say, if the designer used that scale, which for instance does not seem to be the case in
One should therefore always stand on the date line and not on the analemma, even if that is locally suggested by signs or folders. One may use the analemma to estimate the correction for a given date by measuring the distance to the date line off the noon mark along the ellipse. That is to say, if the designer used that scale, which for instance does not seem to be the case in 